Assignment 6

Goals and Background

The main goal of the assignment is to become familiar with regression analysis. During this assignment SPSS will be utilized to calculate the regression output. Additionally, the assignment will provide experience mapping Standardized Residuals using ArcMap and connecting statistics to the resulting spatial output.

Definitions

Regression analysis: is a statistical evaluation of the influence the independent variable has on the dependent variable.

• Can only be done with 2 variables
• Results of regression included the following
• Trendline equation
• Coefficient of Determination (r²)
• explanation variable of how well the dependent variable is explained by the independent variable.
• Range between 0-1, the closer to 1 the higher the dependent variable is explained by the independent variable. 
• Standard Error of the Estimate (SEE)
• Result of the standard deviation of the residuals
• Residuals are how far the points vary from the trendline

Residuals is how far the actual data points deviate from the trendline or the plane (multiple regression). The residuals show which data points are outliers compared to the average in a positive or negative fashion. 

Multiple regression analysis: is a statistical evaluation of the influence of multiple independent variable on a dependent variable.

• Only one dependent variable
• Can have multiple independent variables

Multicollinearity of multiple regression influences the results. Multicollinearity influences your results when two of the independent variables are highly correlated thus pulling the plane of the regression in one direction more than it should. The test for multicollinearity follows the following three test values output in SPSS.

• Eigen Values close to the numerical value of 0 tells the analysis multicollinearity could be present in the data.
• High Condition Indexes (HCI) over the numerical value of 30 tells the analyst multicollinearity is present in the data. However, the HCI does not state which independent variable is causing the multicollinearity
• Variance Properties (VP) close to the numerical value of 1 are the most likely to be causing the multicollinearity.

Part 1

Scenario

I was provided data for a neighborhood which contained the percent of kids that get free lunch in the given areas and the crime rate per 100,000 people.  Then I was provided the following situation:

"A study on crime rates and poverty was conducted for Town X.  The local news station got a hold of some data and made a claim that as the number of kids that get free lunches increase so does crime."

I was then instructed to answer the following questions:

1. Determine if the news stations claim is correct using SPSS?
2. A new area of town was identified to have 23.5% of kids getting free lunch, so what would the corresponding crime rate be? 
3. How confident am I in the results for question 2?

Methods

I completed the regression analysis in SPSS using the Excel file which contained the data for the neighborhood. The Crime Rate was the Dependent variable and the Percent of kids getting free lunch was the Independent variable (Fig. 1).

(Fig. 1) Linear Regression window in SPSS with the inputs of the dependent and independent variables.

Results

(Fig. 2) Regression analysis results from SPSS for % of kids with free lunch (Independent) and crime rate (Dependent).

Looking at the results in Fig. 2 you can see the R Square vale of .173 under the Model Summary heading. The R Squared value of .173 is very low which tells me the % of free lunches does not explain the crime rate for the given neighborhood.  The Sig. level found under the Coefficients heading for PerFreeLunch of .005 has little merit with such a low R Squared value.

Conclusion

Based on the results of the regression analysis the news report was incorrect. Crime rate is not related to the % of children whom get free lunches. I am making an assumption the reported calculated the basic Bivariate Correlation between the variables which resulted in the .005 significance value and a Pearson Correlation of .416. The results of the correlation tells you they are correlated but doesn't tell you why. (For more on correlation see my blog for Assignment 5)  In this case the regression analysis shows the two variables are not "dependent" of each other.

(Fig. 3) Correlation results for % free lunches to crime rates calculated in SPSS.

Part 2

Scenario

I was provided data for 911 calls in Portland, OR. Then I was provided the following scenario:

"The City of Portland is concerned about adequate responses to 911 calls.  They are curious what factors might provide explanations as to where the most calls come from.  A company is interested in building a new hospital and they are wondering how large an ER to build and the best place to build it."

The data I was provided contained the following:

• Calls (number of 911 calls per census tract) 
• Jobs 
• Renters 
• LowEduc (Number of people with no HS Degree) 
• AlcoholX (alcohol sales) 
• Unemployed 
• ForgnBorn (Foreign Born Pop) 
• Med Income 
• CollGrads (Number of College Grads) 

I will answer the following questions for the given scenario:

1. What factors may provide explanation of where the most calls come from in Portland, OR.
2. Where is the best place to build a new ER.

I cannot answer what size of ER to build with the given data so will not be answering that question.

Methods

I utilized SPSS to complete regression analysis using Calls as the dependent variable (Fig. 3). I ran numerous regressions analysis using each of the other variables as the independent variable.

(Fig. 3) Linear Regression window in SPSS with the inputs of the dependent and independent variables. (One of many which were calculated). 

Next, a map was created displaying the number of 911 calls by Census Tract (Fig. 9) in ArcGIS along with a map of the residuals of between the 911 calls and renters (Fig. 10).

Then a multipule regression was ran using SPSS with the Collinearity Diagnostics turned on using the Enter method for the same data which was ran separately (Fig. 11 & 12). Then another multipule regression was calculated using the Stepwise method.

Results

(Fig. 4) Image containing all of the resulting regression analysis for each factor possibly affecting the # of 911 calls.

The regression analysis between Renters and the # of 911 calls stands out the most when looking at all of the results in Fig.4 (Fig. 5). The R-Squared value is .616 which is the highest of all the results. Additionally, the Sig. value is .000 which tells us to reject the null hypothesis which is "The number of renters does not influence the # of 911 calls". Looking at the Constant value one can see for every 1 value the crime rate increases the # of 911 calls increases by 3.8. The R-squared only explains about 60% of the reason for the 911 calls. Looking at the other results such as Unemployed, LowEduc, ForgnBorn also have high R-squared values which help explain additional influencing factors for 911 calls (Fig. 6-8). An assuption to be made is there is some correlation between the other three categories (Unemployed, LowEduc, ForgnBorn) and Renters. However, the question asked was only about the influencing factors on 911 calls so I will not be calculating those values.

(Fig. 5.) Regression analysis results between Renters and # of 911 calls.

(Fig. 6) Regression analysis results between Unemployed and # of 911 calls.

(Fig. 7) Regression analysis results between LowEduc and # of 911 calls.

(Fig. 8) Regression analysis results between Unemployed and # of 911 calls.

(Fig. 9) Standard deviation display of the number of 911 calls in Portland, Oregon.

The blue areas in Fig. 9 are displaying areas which have lower than average 911 calls compared to the average of all the Census Tracts. The brown areas are slightly above the average of 911 calls.

(Fig. 10) Residual display by standard deviation between the # of 911 calls and Renters in Portland, Oregon.

The peach to red colors show residuals which are higher (above the trendline) than the average. You can see the relationship between the 911 calls which are high in Fig. 9 and the peach to red areas of Fig. 10. These areas have a higher relationship between 911 calls and renters for the Portland area.

(Fig. 11) Multiple regression result using the Enter method.

The R-squared value for the multiple regression of .783 shows the strength between the variable is high. Investigating the Standardized Coefficients Beta tells us LowEduc his the best predicting variable for 911 calls as is the highest absolute value. The Beta value shows LowEduc explains ~61% of the 911 calls. The significance level is also .000 which states there is a relationship between the # of 911 calls and LowEduc.

(Fig. 12) Multiple regression collinearity diagnostics result.

Based on the defined parameters above there is no issue with multicollinearity with this set of data.

(Fig. 13) Variable display from the results of the multiple regression analysis using the Stepwise method.

(Fig. 14) Utilized and excluded variables result from the multiple regression using the Stepwise method.

Analyzing Fig. 14 you can see SPSS selected out Renters, LowEduc, and Jobs as the best independent variables which explain the # of 911 calls. These results are very similar to my first analysis with Jobs being the only variation. The single regression analysis pointed me to Unemployed which is obviously closely related to Jobs.  In the third model LowEduc is still the highest predictor of 911 calls in the Portland area due to having the highest Beta value. The Beta value shows LowEduc explains ~46% of the 911 calls while Jobs explain ~34%.

(Fig. 15) Collinearity diagnostics results from the Stepwise method.

Again, based on the above parameters there is no multicollinearity with the values selected by the Stepwise process in SPSS.





Conclusion

There is a slight variation between the methods of regression analysis preformed. The multiple regression using the Enter method using all of the variables shows how factors can influence and alter the results making them less accurate than the Stepwise method. Both methods result in the same independent variable being the primary factor influencing the 911 calls. However, the amount which the variable explained the 911 calls varied between the methods. The variance resulted from the influence of the other variables affecting the plne of the multiple regression.

Assignment 5

Goals and Background

The primary purposes of this assignment is to practice calculating Correlation Statistics using IBM SPSS software and interpret the results of the SPSS combined with an Excel Scatterplot of the same data.

Correlation is the measurement of the association between two variables. One cannot measure the correlation of more than two variables. Correlation results informs the analyst about the strength of the association and also the direction of the association. Correlation results are always between -1 and 1. The closer to actual -1 or 1 the stronger the association. If the correlation result is 0 then there is no correlation association or a null relationship. A positive relationship is when the value of one variable increases and the value of the other variable increases as well. A negative relationship would be when the value of one variable increases the other variable decreases.

Part 1

I was provided data from the Census Tracts which were focused around categories for the Population in Milwaukee, WI. My directions were to explain the patterns found using the correlation matrix.

The data was provided to me in an Excel Spreadsheet. 

Below were the categories of data I was provided:

• White  = White Pop. for the Census Tracts in Milwaukee County
• Black = Black Pop
• Hispanic = Hispanic Pop
• MedInc = Median Household Income
• Manu = Number of Manufacturing Employees
• Retail = Number of Retail Employees
• Finance = Number of Finance Employee

I opened the Excel file in SPSS and preformed the Bi-variate Correlate using Pearson Correlation on all of the categories of the data. Correlation can only be preformed on two categories at a time. SPSS creates a correlation matrix comparing all of the categories against each other (Fig. 1).

(Fig. 1) Correlation Matrix created in SPSS from the Excel Spreadsheet I was provided. Note the comparison only calculated the correlation between two categories.

Analyzing the correlation matrix one needs to look at the Pearson Correlation value. The closer the value is to -1 or 1 the stronger the correlation is. The highest Pearson Correlation value is between White and Manu with a .735. The value states there is a high positive correlation between the white population and the number of manufacturing employees. To better understand the correlation I created a scatter plot in Excel to visualize the trend (Fig. 2). 

(Fig. 2) Scatterplot created in Excel displaying the correlation trend between the white population and manufacturing jobs.

Analyzing the scatterplot you can see there is a positive relation between the white population and manufacturing jobs. The one thing correlation results cannot do is identify the causation of the trend. The trend could be merely coincident also called a spurious relationship.

Looking back at the matrix note there are some negative values. The negative values are designating a negative relationship. I created a scatterplot to display the relationship between the black population and the median household income which had the "highest" negative value (Fig. 3).

(Fig. 3) Scatterplot created in Excel displaying the correlation trend between the black population and median household income.

Looking at Fig. 3 you can see the negative correlation is not as distinct as Fig. 2. Which is also portrayed by the Pearson Value. -.417 is farther away from -1 than .735 is from 1 thus the variation between the two scatterplots.

Part 2

Introduction

I was provided data containing  Democratic votes and voter turnout for all the counties in Texas from the Texas Election Commission (TEC) for the 1980 and 2016 Presidential Elections. The data codes are as follows:

• VTP80 = Voter Turnout 1980
• VTP16 = Voter Turnout 2016
• PRES80D = % Democratic Vote 1980
• PRES16D = % Democratic Vote 2016

I was also instructed to download the percent of Hispanic populations for all the counties in Texas from the 2015 U.S. Census 2015 ACS Data.

Scenario 

The TEC has requested and analysis of the patterns of the election to determine if there is clustering of the voting patterns and voter turnout. The TEC wants to present my findings to the governor to see if the election patterns are different than they were 36 years ago. 

Methods

I utilized SPSS to run Bi-variate correlation using the Pearson method on the data I was provided. The resulting correlation matrix can be seen in Fig. 5.

I created two scatterplots of the correlation data to help better understand what the matrix is detailing. The first scatterplot displays the correlation between the 1980 percent Democratic vote and the 1980 voter turnout (Fig. 6). The second scatterplot displays the correlation between the 2016 percent Democratic vote and the 2016 voter turnout (Fig. 7).

The second form of analysis was preformed with a program called GeoDa to preform Spatial Autocorrelation on both years of voting data and the Hispanic population. Spatial Autocorrelation is different than regular correlation as it calculates the correlation of a singular variable through space against neighboring areas of the same distinction. Spatial Autocorrealtion compares neighboring areas (counties in this case) to each other to determine if they are "more alike" (positive), "unlike" (negative), or "random" (no spatial autocorrelation).

Spatial Autocorrelation with GeoDa was used to calculate Moran's I. Moran's I is an indicator of spatial autocorrealation. The results of Moran's I ranges between -1 and 1. The closer to 1 the more clustered the variable is said to be in a specific zone. The closer to -1 the less clustered (dispersion) the variable is said to be in a specific zone. Examining Fig. 4 you can see examples of exact -1 and 1 spatial autocorrelation. Vary rarely if ever will you see exact (perfect) spatial autocorrelation. I will utilized a map of the Texas counties to display the spatial autocorrelation calculated by GeoDa along with a Moran's I chart and value. The maps are color coded to display the clustering of the counties. Bright Blue denotes areas of low value surrounded by other areas of low value. Bright Red denotes areas of high value surrounded by other areas of high value. Light blue denotes areas which are low in value surrounded by areas of high value. Light red or periwinkle denotes areas of high value surrounded by areas of low value. The light blue and light red are the outliers in the clustering analysis.

(Fig. 4) Graphic displaying less clustered (-1) and more clustered (1) spatial autocorrelation. Image obtained from https://glenbambrick.com/tag/morans-i/.

Results

(Fig. 5) Correlation matrix for TEC data.

(Fig. 6) Scatterplot of 1980 voting data comparing the percent of democratic vote to the voter turnout.

Analyzing the scatterplot from the 1980 voting data comparing the percent democratic vote to the voter turnout you can see there is a negative correlation. The negative correlation shows as the voter turnout decreases the percent of Democratic vote increases. The Pearson's value of -.612 from SPSS tells us this is a Moderate correlation between the two values.

(Fig. 7) Scatterplot of 2016 voting data comparing the percent of democratic vote to the voter turnout.

Analyzing the scatterplot from the 2016 voting data you can see the same negative correlation as the 1980 data though not as correlated. The decrease in correlation is backed up by the Pearson's value of -.530 which is still a Moderate correlation but is less than the 1980 data.

1980 Percent Democratic Vote

(Fig. 8) Moran's I value and chart for 1980 Democratic vote.

(Fig. 9) 1980 LISA Cluster Map for 1980 Democratic vote.

Investigating the Spatial Autocorrelation of the 1980 Democratic vote we obtained a Moran's I of .575 (Fig.8). The numeric value tells us there is a slight Spatial Autocorrelation between the counties and the Democratic vote. However, the value is still about half way to one so the correlation is not very high. The map displays clustering of high Democratic voting in the Southern Tip (Fig. 9), and a few counties in far Eastern Texas. A large amount of clustering for counties which had low Democratic vote reside in the Northern portion of the state extending down slightly to the central portion.

2016 Percent Democratic Vote

(Fig. 10) Moran's I value and chart for 2016 Democratic vote.

(Fig. 11) LISA Cluster Map for 2016 Democratic vote.

Analyzing the 2016 Democratic vote we seen an increase in the Moran's I value to .685 (Fig. 10). The values tells us there is an increase in clustering over the 1980 data. The increased clustering can be seen in Fig. 11 with more of the counties being designated by various colors. Note the shift of the Low-Low (blue) from the West side to the East side of North Central Texas. The map displays a shift in voting tendencies of those counties. The counties with high Democratic voting are still primarily located in the Southern tip of the state just like the 1980's data.

1980 Voter Turnout

(Fig. 12) Moran's I value and chart for 1980 voter turnout.

(Fig. 13) LISA Cluster Map for 1980 voter turnout.

The 1980 voter turnout analysis shows clustering in certain areas but with a Moran's I value of .468 the clustering is minimal but note worthy is specific areas (Fig.12). One can see even less counties are colored in which is tied directly to the lower Moran's I value than the previous two examples (Fig. 13). You can see a large cluster of counties which had low voter turnout in the Southern tip of the state. The low voter turnout relates back to the first scatterplots which showed the negative correlation between voter turnout and democratic vote when comparing with the 1980 Democratic vote map. The same can be said for the counties in the Eastern part of the state which had low voter turnout.

2016 Voter Turnout

(Fig. 14) Moran's I value and chart for 2016 voter turnout.

(Fig. 15) LISA Cluster Map for 2016 voter turnout.

The 2016 voter turnout has the lowest Moran's I of all the data thus far with a value of .287 (Fig 14). Again there is clustering in a few areas throughout the state but for the most part no real specific patterns are seen in the map (Fig. 15). Again we see low voter turnout in the southern tip of the state which ties back to the high Democratic vote from previous map.

Percent Hispanic Population

(Fig. 16) Moran's I value and chart for 2015 percent Hispanic Population.

(Fig. 17) LISA Cluster Map for 2015 percent Hispanic Population.

Analyzing the percent of Hispanic population across Texas displays the highest clustering of all the data. The Moran's I value is .779 (Fig. 16), which is a high value stating there is high clustering of counties with low percentages of Hispanic populations and high clustering of counties with high percentages of Hispanic populations. There is a high percentage of Hispanics along the southern edge of Texas which boarders Mexico (Fig. 17). The North East portion of Texas has lower than average populations of Hispanics with the exception of the one periwinkle county in the middle. My professor stated there is a large carpet factory in that county which employs many Hispanic workers thus many Hispanics live there.

Discussion and Conclusion

Comparing the 1980 voter turnout to the 1980 Democratic vote LISA Map you can better see the correlation using the Spatial Autocorrelation display (Fig. 18). The Southern tip of Texas shows a distinct correlation between voter turnout and the Democratic vote. The Northern portion of the state has some correlation between the two but not nearly as high as the Southern Tip. The same could be said about the Eastern portion of the state. There was definitely some clustering in the voting patterns in Texas during the 1980's elections as displayed by the LISA Maps.

(Fig. 18) LISA maps for 1980 voter turnout (Left) and 1980 Democratic vote (Right).

The 2016 comparison of the voter turn out to the Democratic vote displays a similar pattern though shifted to the East a bit for the Democratic vote (Fig. 19). The shift could be attributed to growing population closer to Dallas and Fort Worth Texas which reside in the North Eastern Portion of the main body of Texas (Fig. 20).

(Fig. 19) LISA maps for 2016 voter turnout (Left) and 2016 Democratic vote (Right).

(Fig. 20) Locations of major cities in Texas taken from Google Maps.

The analysis I provide will be useful for target campaigns for specific "parties" (Republican or Democrats). Additionally, the areas with low voter turnout could be targeted for "Get out and vote" campaigns. Additional research is required to see the influencing factors which are causing the clustering in specific locations. Also, why the negative correlation holds true in some counties but not others. Lastly the counties which are "outliers" that go against the clustering of surrounding counties could be investigate for specific reasoning's. 

Assignment 4

Goals and Background

The purpose of the following assignment is to become familiar with "z" and "t" tests as a method of hypothesis and significance testing of gathered data. Deciphering which test to use, calculation of the actual test, and interpretation of the data will be discussed in the following post utilizing various examples.

Hypothesis and significance testing is a useful way to support the interpretations of research data and conclusions. While the testing does not prove the research to be a fact, it does provide additional evidence to support ones theories. The result of hypothesis testing only tells you if there is a difference between two sets of data and nothing more. The results DO NOT tell you how they are different. To understand how they are different you must return to the original data entered in the equation for analysis. 

Terms

Steps of Hypothesis Testing

1. State the null hypothesis
2. State the alternative hypothesis
3. Choose a statistical test
4. Choose the significance level (α)
5. Calculate test statistic
6. Make a decision about the null & alternative hypothesis

Null Hypothesis

A null hypothesis states there is NO significant difference between the sample mean (smaller portion of a larger data set) and the mean of the entire population which you are comparing the data against. Example would be comparing one Major League Baseball (MLB) (sample mean) team against the entire MLB as a whole (entire population).

Alternative Hypothesis

A alternative hypothesis states there IS a significant difference between the sample mean (derived from personal data) and the mean of the entire population which you are comparing the data against.

*The selection of the null or alternative hypothesis only tells you there is a difference and DOES NOT tell you by how much the difference is.*

**Either "Reject" or "Fail to Reject" the null hypothesis, NEVER "accept" the null hypothesis. Additionally, do not "Reject" or "Fail to Reject"the alternative hypothesis.

Type 1 Errors

Type 1 errors happen when a true (Fail to Reject) null hypothesis is rejected, which is also know as a false positive.

Type II Errors

Type II errors is the opposite or a false negative as compared to the false positive of the Type I error.

Significance Level (α)

Significance level is set during hypothesis testing to determine the likelihood/probability of Type I errors occurring. The level is set based on the confidence interval. An example of a typical significance level is .05. If a significance level is set to .05, it states that 95% of the time a Type I error will not occur. The significance level is used to determine the critical value. For a one tailed test you can leave the significance level alone, however for a two tailed test you have to divide the level in half. Example if you were given a Confidence Interval of 95% you would have to divided the last 5% by 2 which would give you a significance interval of .025.

Confidence Intervals (CI) 

The Confidence Interval (CI) is the range of number which fall between critical values of a two-tailed test or the majority of the normal distribution of a one tailed test (Fig. 1)

(Fig. 1) The white area under the normal distribution would be the Confidence Interval (CI) of a hypothesis test. The image shows a one tailed & a two tailed test. Image collected from https://www2.ccrb.cuhk.edu.hk/stat/User%20guidance,%20definition%20and%20terminology%20(Online%20Help).htm. 

Critical Value (CV)

The Critical Value (CV) is the exact numeric location on the normal distribution which divides the "reject" (black area of Fig. 1) and "fail to reject" (white area of Fig. 1). If a test statistic is below the CV then the test fails to reject the null hypothesis. Alternatively if a test statistic is above the CV then the test rejects the null hypothesis.

z-test

A z-test is utilized to determine if the average of 2 population data sets are statistically different (Fig. 2). One of the data sets must be a smaller representation of samples (sample mean) compared to the other (population mean). Z-tests are generally used for samples sizes larger than 30 (n). For the purposes of this assignment we will be using the same chart as we did in Assignment 3 to calculate the CV for our z-tests.

(Fig. 2) Formula used for a z-test. Image collected from http://isoconsultantpune.com/hypothesis-testing/.

t-test

T-test utilize the same formula as a z-test but when determining the CV one must utilize Degrees of Freedom to calculate. The Degrees of Freedom are calculated by subtracting 1 from the total number of test samples (n) and finding the corresponding value with you significant level (α). T-tests are used from sample sizes smaller than 30. For the purposes of this assignment we will be using a chart provided in our book to determine the CV (Fig. 3).

(Fig. 3) T-test chart from Statistical Methods for Geography by Peter A. Rogerson utilized for this assignment.

Part 1: t and z test

Question 1

I was provided a chart which contained the Interval Type, Confidence Interval (labeled as Confidence Level in this case), and the number of test samples (n) (Fig. 4). From this information I was to determine which test type was appropriate and the Significance Level (α). Using the descriptions from the above terms I was able to determine the missing values which are highlighted in gold in Fig. 4. Notice for the two-tailed tests there are 2 z or t values.

(Fig. 4) Table with the provided information highlighted in blue and the information I determined highlighted in gold.

Question 2

The following question/scenario was provided to me:

1.       A Department of Agriculture and Live Stock Development organization in Kenya estimate that yields in a certain district should approach the following amounts in metric tons (averages based on data from the whole country) per hectare: groundnuts. 0.57; cassava, 3.7; and beans, 0.29.  A survey of 23 farmers had the following results: (10 pts)                                                 μ             σ                Ground Nuts         0.52        0.3                Cassava                 3.3          .75                Beans                    0.34        0.12        
a.       Test the hypothesis for each of these products.  Assume that each are 2 tailed with a Confidence Level of 95% *Use the appropriate testb.       Be sure to present the null and alternative hypotheses for each as well as conclusionsc.       What are the probabilities values for each crop?
d.       What are the similarities and differences in the results 

I followed the steps of hypothesis testing to answer the majority of the questions.

1. State the null hypothesis
1. There is no difference between the average of Ground Nuts harvested (metric tons/hectare) from the 23 sampled farmers compared to the whole country average of harvested Ground Nuts (metric tons/hectare).
2. There is no difference between the average of Cassava harvested (metric tons/hectare) from the 23 sampled farmers compared to the whole country average of harvested Cassava (metric tons/hectare).
3. There is no difference between the average of Beans harvested (metric tons/hectare) from the 23 sampled farmers compared to the whole country average of harvested Beans (metric tons/hectare).
2. State the alternative hypothesis
1. There is a difference between the average of Ground Nuts harvested (metric tons/hectare) from the 23 sampled farmers compared to the whole country average of harvested Ground Nuts (metric tons/hectare).
2. There is a difference between the average of Cassava harvested (metric tons/hectare) from the 23 sampled farmers compared to the whole country average of harvested Cassava (metric tons/hectare).
3. There is a difference between the average of Beans harvested (metric tons/hectare) from the 23 sampled farmers compared to the whole country average of harvested Beans (metric tons/hectare).
3. Choose a statistical test
1. Since there are 23 farmers (n=23) I will utilize a t-test.
4. Choose the significance level (α)
1. Based on a Confidence Level of 95% and need to perform a 2 tailed test the significance level (α) is equal to .025.
2. The critical value is then determined to be 2.074 based on a significance level of .025 and the Degrees of Freedom (23-1=22) chart.
5. Calculate test statistic
1. Ground nuts: t=(.52-.57)/(.3/sqrt(23))=-.05/.063=-.794
2. Cassava: t=(3.3-3.7)/(.75/sqrt(23))=-.4/.156=-2.56
3. Beans: t=(.34-.29)/(.12/sqrt(23))=.05/.025=2
6. Make a decision about the null & alternative hypothesis
1. Ground nuts: Failed to reject the null hypothesis
2. Cassava: Reject the null hypothesis
3. Beans: Failed to reject the null hypothesis

The probability values for each crop are as follows:

1. Ground nuts: .78344
2. Cassava: between .98938 & .99144 
3. Beans: .97037

The similarities between the results are both Ground Nuts and Beans failed to reject the null hypotheses. The failure to reject tells us there is no difference between the sample mean and the hypothesized mean for either crop. The differences between the results are related to the Cassava which did reject the null hypothesis. The rejection of the null hypothesis tells me there is a difference between the sample mean compared to the country average. Examining the probabilities for each crop you can see the Bean probability is between 1-2% different than Cassava. Additional samples may need to be acquired to provide a better representation of the Bean crop in Kenya.

Based on the original statement it is not wise to utilize the country wide estimates for Cassava harvests in Kenya. The harvest estimates for Cassava should be examined more extensively to set their own local yield estimates. The harvest yield estimates for Beans and Ground Nuts are acceptable for Kenya.

Question 3

The following question/scenario was provided to me:

A researcher suspects that the level of a particular stream’s pollutant is higher than the allowable limit of 4.2 mg/l.  A sample of n= 17 reveals a mean pollutant level of 6.4 mg/l, with a standard deviation of 4.4.  What are your conclusions?  (one tailed test, 95% Significance Level) Please follow the hypothesis testing steps.  What is the corresponding probability value of your calculated answer? 

Again I followed the steps of hypothesis testing to answer the majority of the question.

1. State the null hypothesis
1. There is no difference between the sample mean of the specific stream and the allowable limit of streams pollutants.
2. State the alternative hypothesis
1. There is a difference between the sample mean of the specific stream and the allowable limit of streams pollutants.
3. Choose a statistical test
1. With a (n) value of 17 I will be utilizing a t-test.
4. Choose the significance level (α)
1. With a Confidence level of 95% and preforming a one-tailed test the significance level is equal to .05. Utilizing the significance level and Degrees of Freedom the critical value is equal to 1.746.
5. Calculate test statistic
1. t=(6.4-4.2)/(4.4/sqrt(17))=2.2/1.067=2.062
6. Make a decision about the null & alternative hypothesis
1. I reject the null hypothesis.

The corresponding probability value of my calculated answer is between .97403 & .97858. The probability tell me that between 97.4% and 97.8% of the time the calculation of rejecting the null hypothesis is correct. So I can say with ~97% confidence there is a difference between the stream sample and the allowable limit of pollutants. Looking back at the original data I can see the pollutant level of the sample stream is higher than the allowable limit. The result would make me inquire of why the pollutants of the stream are higher. I would look for possible sources contributing to the increased pollution.

Part II

I was provided a shapefile with average housing values by Block Group for Eau Claire County Wisconsin. I was then provided a shapefile with average housing values by Block Group for just the City of Eau Claire. I was given the following question to answer from the data:  "Is the average value of homes for the City of Eau Claire block groups significantly different from the block groups for Eau Claire County?"

Utilizing the housing value information attached to the shapefile I calculated the mean for both the city and the entire county. The average for the city block groups was $151,876.51 and the average for the entire county was $169,438.13. The standard deviation for the city block groups was $49,706.92. There were 53 block groups within the city of Eau Claire. With this information I was prepared to complete the steps for hypothesis testing.

Steps for hypothesis testing:

1. State the null hypothesis
1. There is no difference between the average housing values for the city of Eau Claire, WI compared to the entire county of Eau Claire, WI.
2. State the alternative hypothesis
1. There is a difference between the average housing values for the city of Eau Claire, WI compared to the entire county of Eau Claire, WI.
3. Choose a statistical test
1. There are 53 block groups in the city of Eau Claire, so I will be utilizing a z-test.
4. Choose the significance level (α)
1. I was given a Confidence level of 95% and will be using a one-tailed test, so the significance level is .05. Using the previous information I have calculated a critical value of -1.64 (negative because as you will see my calcualted result for my test statistic is a negative value).
5. Calculate test statistic
1. z=(151876.51-169438.13)/(49706.92/sqrt(53))=-17561.62/6827.77=-2.57
6. Make a decision about the null & alternative hypothesis
1. I will reject the null hypothesis.

Rejecting the null hypothesis states there is a statistical difference between the City of Eau Claire average housing values compared to the entire Eau Claire County. The hypothesis test does not tell us much about the difference besides being below the average for the county based on the negative test statistic. Looking back at the calculated mean values you can see the city block group difference is $17,561.62 less than the Eau Claire County as a whole.

I created a map to display the variation of housing values across the entire county (Fig. 5). I used a standard deviation classification for the purpose of trying to locate a pattern which would support the above hypothesis test. The map plainly displays all of the block groups in the county which are below the average are located in the City of Eau Claire block group. The map combined with the statistical test stating there is a difference between the city and the county as a whole provides evidence need to investigate why there is a difference between the two.

(Fig. 5) Display of average home values by county block groups of Eau Claire County, Wisconsin.

Assignment 3

Goals and Background

The purpose of the assignment is to provide us with experience calculating Z-Scores and Probability for a given data set. Additionally, the assignment will provide experience relating the calculated information (Z-Scores and Probability) to a given scenario for pattern analysis.

Terms

Z-Score: A Z-Score is the the precise number of a standard deviation which a specific observation lies on the standard deviation curve. If a numeric value lies between 1 and 2 standard deviations on the curve, using the Z-Score formula (Fig. 1) will calculate the exact location.

(Fig. 1) Z-Score formula. Zi: Z-Score, Xi: observation value, u: mean of the data, S: standard deviation of the data.

Probability: Probability can be described as the likelihood (by percent) a numeric valued event will occur. The probability is calculated from the z-score via a probability chart (Fig. 2). Z-Scores can also be calculated in Microsoft Excel and a host of other programs. Probability is calculated from absolute frequency of a specific event occurring compared to the all of the events in the data.

(Fig. 2) Probability chart based on Z-Scores.

The Scenario

     You have been hired by an independent research consortium to study the geography of foreclosures in a Dane County, Wisconsin.  County officials are worried about the increase in foreclosures from 2011 to 2012.  As an independent researcher you have been given the addresses of all foreclosures in Dane County for 2011 and 2012 and they have been geocoded and then added to the Census Tracts for Dane County.    While you realize that you cannot determine the reasons for foreclosures occurring, you do have the tools to analyze them spatially.  Specifically, you are interested to see how the patterns of these foreclosures have changed from one year to the next.  Explain what the patterns are and also provide some understanding as to the chance foreclosures will increase by 2013?  

A second question is to be answered after calculating the Z_Score for three specific Tracts located in Dane county.

If these patterns for 2012 hold next year in Dane County, based on this Data what number of foreclosures for all of Dane County will be exceeded 70% of the time?  Exceeded only 20% of the time?  

Methods

The first step was to create a map displaying the change between 2011 and 2012 for Dane County using ArcMap. I added a field to the attribute table and subtracted the 2012 foreclosure value from the 2011 value for each tract. The result was displayed using standard deviation classification (Fig. 4).

(Fig. 3) Display of locations of selected Census tracts 114.01, 122.01, and 31.

The next step the instructions was to calculate the Z-Score for 3 select tracts in the data (Fig. 3). I utilized ArcMap to extract the Mean and the Standard Deviation for both years of data. I then extracted the values for the specific tracts from both years and input all of the values in Microsoft Excel. The Z-score was then calculated using Excel (Fig. 5).

Results

(Fig. 3) Display of the foreclosure change between 2011-2012 by Census Tract in Dane County.

Examining the map you can decipher the areas which have had a significant increase in foreclosures are illustrated by the dark/bright red color. Alternatively, the areas in darker blue have seen an decrease in foreclosures since 2011. Areas with increased foreclosures seem to be outside of the downtown/capital area (see Fig. 3 for location), though there are a few outside the capital which have lower foreclosures. More information is required to decipher why this pattern is emerging.

(Fig. 4) Excel spreadsheet with the Z-Score calculation data and results.

(Fig. 5) Display of 2011 foreclosures by standard deviation classification.

Fig. 5 is a map displaying the foreclosure numerical value for 2011 with a standard deviation classification. The standard deviation calculates the Z-Score for each value and assigns it to the proper classification representation. Tract 114.01 has a higher amount of foreclosures compared to the average of the county. Tract 31 has a slightly higher amount of foreclosures compared to the average of the county. Tract 122.01 has a slightly lower number of foreclosures compared to the county average. These representations are correlated by the results I calculated in the Excel sheet (Fig. 4). Comparing these results to Fig. 3 shows a few note worthy observations. The central northern most tract displays a higher than average amount of foreclosures but in Fig. 3 it had a significant reduction in foreclosure numbers. The same observation can be made for the large tract east of Tract 114.01 but not as much of a significant change between 2011 and 2012.

(Fig. 6) Display of 2012 foreclosures by standard deviation classification.

Fig. 6 is a map displaying the foreclosure numerical value for 2012 with a standard deviation classification. The results are essentially the same between the 3 selected tracts. Though the Z-Score for Tract 31 decreased a fair amount from 2011 it still fell in the .5-1.5 Std. Dev. Same as the 2011 results there are a few anomalies which appear when comparing the change between the 2 years and the Z-Score map though not as easy to identify.

Finally I will answer the following question:

If these patterns for 2012 hold next year in Dane County, based on this Data what number of foreclosures for all of Dane County will be exceeded 70% of the time?  Exceeded only 20% of the time?  

Foreclosures with a Z-Score greater than a -.52 will be exceeded 70% of the time. This equates to 70% of the time the foreclosures for a given tract will exceed approximately 7.

Foreclosures with a Z-Score greater than .84 will be exceeded 20% of the time. This equates to 20% of the time the foreclosures for a given tract will exceed approximately 20.

Conclusion

A pattern of higher foreclosures seems to fall outside of the downtown/capital area of Dane county. While more information is need to fully analyze why this pattern is being displayed I have my own assumptions. There was a significant housing market crash around these years due to a dwindling economy. People whom moved from the inner city to more posh suburbs bought houses which they could no longer afford when they lost their jobs. Thus many homes went into foreclosure in these areas. Again, this is merely a guess and more research would be required to verify that claim.

Analyzing the change between years doesn't give you the full picture of what is going on with the data. Calculating the Z-Scores or creating a standard deviation classified map provides additional information which is critical when attempting to interpret data. Like in the case of the central most northern Tract in Dane county which showed a decrease in foreclosures but still was above the average for the county. The observation tells you there is more to investigate in the area to gain a full understanding of what is going on. These observations combine with further data from more recent years would be very beneficial to many government agencies in Dane County.

Assignment 2

Goals and Background

The goal of the following assignment is to become familiar with a variety of statistical methods including Range, Mean, Median, Mode, Kurtosis, Skewness, and Standard Deviation. Additionally, the assignment will provide practice using computer programs including Microsoft Excel and ESRI Arc Map to complete calculations of statistical methods.

Definitions

Before beginning the assignment me I will define and explain a few of the statistical methods used in the assignment. The terms are described in relationship to research data sets where you almost never have a perfectly even or normally distributed data.

Range

Range is the difference between the the largest value and the smallest value in a set of data. Example if you had the data set 4,3,2,1, the range would be equal to 4-1, which is obviously 3.

Mean

Mean is average of all the numbers in a given data set. The mean is calculated by adding all of the numbers together and dividing the total by the total numbers of values in the data set. Example if you had the 4,3,2,1 data set you would first 4+3+2+1= 10. Then you would divide 10 by 4 which would give you a mean value of 2.5.

Median

Median is the number which falls in the middle of a data set when put in order from smallest to largest. Example 1,2,3,4,5 the median would be 3. The previous example is when the total of number of values is odd. Should your data set values total an even number you take the mean of the middle two numbers. Example 1,2,3,4, you would fine the mean of 2,3 which would make the median 2.5.

Mode

Mode is the number which occurs most often in a data set. Example 1,2,3,4,4, the mode would be 4. It is possible to have multiple modes depending on the values of the data set. 

Normal Distribution

A normal distribution is a describing term which states the majority of the data clusters around the mean. Gaussian Distribution is another term which means the same thing. Normal distributions are theoretical and displayed by a histogram (Fig. 1).

(Fig. 1) Image of a normal distribution histogram. Image source: http://www.oxfordmathcenter.com/drupal7/node/300.

Skewness

Skewness describes the balance of the histogram compared to a normal distribution. There are 3 types of skewness: positive, no skew, negative (Fig. 2). Positive skew is when the outliers in a data set are on the positive side of the mean. Negative skew is when the outliers are on the negative side of the mean. No skew means there is an even distribution of the data. When analyzing skew anything below 1 and above -1 is "acceptable".

(Fig. 2) Image displaying the 3 types of skewness. Image source: http://www.managedfuturesinvesting.com/managed-futures/news/aisource-news/2015/10/13/what-is-skewness.

Kurtosis

Kurtosis describes the shape of the histogram in relation to the steepness of the distribution compared to the theoretical "normal distribution. Leptokurtic, Mesokurtic, and Platykurtic are 3 different terms which describe Kurtosis. Leptokurtic is a description of a very peaked distribution. Mesokurtic is the description of a "normal distribution. Platykurtic describes a flat distribution. Additionally, Platykurtic is described as negative Kurtosis and Leptokurtic is positive Kurtosis.  An example of all three types of Kurtosis can be seen in Fig. 3. When analyzing Kurtosis calculations anything greater than 1 is Leptokurtic and below -1 is Platykurtic.

(Fig. 3) Image displaying the various forms of Kurtosis. Image source: http://mathsstatistics.weebly.com/unit-2.html.

Standard Deviation

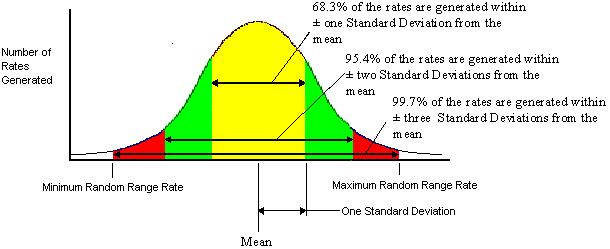
Standard Deviation is a statistical measurement which describes how spread out the numbers in a data set are from the mean. "1 Standard Deviation" from the mean is equal to 68.2% of the values in a data set. "2 Standard Deviations" from the mean is equal to 95.4% of the values in a data set.  "3 Standard Deviations" from the mean is equal to 99.7% of the values in a data set. See Fig. 4 for a visual representation of standard deviation. Standard deviations can go well past 3 depending on the data set.

(Fig. 4) Graphical representation of standard deviations. Image source: http://www.jlplanner.com/html/stddev.html.

 There are 2 different ways to calculate standard deviation. If you have a complete data set (one which is not missing any data) you utilize the population standard deviation formula (Fig. 5). If you have a incomplete data set (missing some values or you were not able to sample everyone/everything) you utilize the sample population standard deviation formula (Fig. 6).

(Fig. 5) Population standard deviation formula. Image source: https://thekubicle.com/lessons/variance-and-standard-deviation.

(Fig. 6) Sample population standard deviation formula. Image source: https://spreadsheetsolving.com/sample-standard-deviation/.

Assignment Description (Part 1)

For the assignment I was given the following scenario:

Cycling is often seen as an individual sport, but it is actually more of a team sport.  You are looking to invest a large sum of money into a cycle team.  While having a superstar is nice and brings attention, having a better team overall will mean more money in your pocket.  In the last race in the TOUR de GEOGRAPHIA, the overall individual winner won $300,000, with only 25% going to the team owner, but the team that won, gained $400,000 in a variety of ways, with 35% going to the team owner.  

Using the incredible set of knowledge learned in your Quant Methods class at UWEC, you decide to put it to good use.  You have data (total time for entire race) for teams and individual racers over the last race held in Spain. To begin your investigation you are to analyze the race times of members from the team. Traditionally Team ASTANA has typically produced the race winner (meaning the rider that finishes first), but an up and coming group named Team TOBLER has been making waves on the cycling circuit.     

The question I am to answer is the following:

Should you invest in Team ASTANA or gamble on Team TOBLER?   Why did you pick one team over another?  What descriptive statistics do you think best help explain your answer?  Please explain your results using the statistics to support your answer **Please explain results in hours and mins. 

(Fig. 7) Data of race times provided to me by my professor.

Methods

For this assignment I had to calculate the Range, Mean, Median, Mode, Kurtosis, Skewness, and Standard Deviation for the race times provided to me. I was instructed to calculate the Standard Deviation by hand and all of the other values could be calculated in Excel.

I copied the provided data and imported it into Excel so I could sort the numbers in descending order. I then copied each teams times on my paper. I then calculated the Range, Mean, Median, Mode, Kurtosis, Skewness for each team using Excel.

The next step was to calculate the standard deviation for each team (Fig. 8-9). Since I was provided all of the times for each team I then utilized the "Population Standard Deviation" formula.

(Fig. 8) Hand calculations of Team Tobler standard deviation.

(Fig. 9) Hand calculations of team Astana standard deviation.

The final step was to analyze the results from the calculations to answer the questions. Additionally, I utilized Excel to verify my hand calculations were correct.

Results

(Table 1.) Results of calculations for the race teams.

Discussion and Answer

I don't feel as I have enough data to answer the question I was given. One race result is not enough for me to make a determination of which team I would invest money in. Additionally, I don't know how the scoring is calculated for the finishers which plays into which team would be the overall winner. The final question I would have is how my investment is paid back. With a higher percentage going to the "owner" does my return come from the owner or the team amount? However, I still have to pick a team for the purpose of the assignment and provide an explanation.

I would choose Team Astana based off the data I was provided. The total time (sum) was equal to 569 hours and ~10 minuets compared to Tobler which had a total time of 571 hours and ~21 minuets. While Team Astana had a shorter overall time, I am not sure how points are awarded for the team results. If consistency and closeness in relationship to other members of the team plays into the calculation I would change my answer to Tobler. The Kurtosis result for team Tobler was higher meaning the team members finished very close together. Additionally, the low standard deviation displays the closeness which team Tobler finished with each other.  Even though team Tobler had a lower standard deviation meaning the team finished the race closer to each other, the majority of team Tobler finished behind team Astana. The high standard deviation of Astana was related to racer K who finished 20 minuets behind anyone from either team. More data would be need to see if this was a normal occurrence or if racer K just had a bad day or had possibly crashed during the race. Finally, the negative Skewness for Tobler tell me more people finished behind there were a few people behind the average which helps display why the majority of Tobler finished behind Astana.

Part 2

Part 2 of the assignment will have me calculating the mean center and a weighted mean center for the population of Wisconsin by county for 2000 and 2015. First I will provide definitions for both terms before displaying and discussing the results which will be displayed on a map.

Mean Center

Mean center is the average "location" of points which have an X and a Y value and are plotted on a graph or Cartesian Plane (Fig. 10).

(Fig. 10) Image displaying a calculated mean center for X,Y coordinates. Image source: http://resources.esri.com/help/9.3/arcgisdesktop/com/gp_toolref/spatial_statistics_tools/mean_center_spatial_statistics_.htm

Weighted Mean Center

Weighted mean center is based off the average like "mean center". However, weighted mean center the points have weights assigned to them by "frequencies" or numbers attached to them. Example if the points had populations data attached to them, the higher the population the higher the weight would be attached to a given point (Fig. 11).

(Fig. 11) Image displaying the difference in mean center and weighted mean center. Image source: http://support.esri.com/other-resources/gis-dictionary/term/weighted%20mean%20center

Results

Discussion

You can see the "mean center" is centrally located in the state when analyzing the map in the results section. The mean center is calculated off of the center point of each county, which is why it is located in the center of the state. However, you can see the weighted mean centers are south and a little to the east of the mean center. The weighted mean center takes into consideration the population of the counties. The reasoning for the shift in placement would be the higher populations in southern portion of the state specifically Milwaukee area which is on the south east border of the state. The 2015 weighted mean center moved slightly to the north and the west. The increase of people working in Twin Cities and living the western portion of Wisconsin is one possible cause of this shift.