The goal of the following assignment is to become familiar with a variety of statistical methods including Range, Mean, Median, Mode, Kurtosis, Skewness, and Standard Deviation. Additionally, the assignment will provide practice using computer programs including Microsoft Excel and ESRI Arc Map to complete calculations of statistical methods.
Definitions
Before beginning the assignment me I will define and explain a few of the statistical methods used in the assignment. The terms are described in relationship to research data sets where you almost never have a perfectly even or normally distributed data.
Range
Range is the difference between the the largest value and the smallest value in a set of data. Example if you had the data set 4,3,2,1, the range would be equal to 4-1, which is obviously 3.
Mean
Mean is average of all the numbers in a given data set. The mean is calculated by adding all of the numbers together and dividing the total by the total numbers of values in the data set. Example if you had the 4,3,2,1 data set you would first 4+3+2+1= 10. Then you would divide 10 by 4 which would give you a mean value of 2.5.
Median
Median is the number which falls in the middle of a data set when put in order from smallest to largest. Example 1,2,3,4,5 the median would be 3. The previous example is when the total of number of values is odd. Should your data set values total an even number you take the mean of the middle two numbers. Example 1,2,3,4, you would fine the mean of 2,3 which would make the median 2.5.
Mode
Mode is the number which occurs most often in a data set. Example 1,2,3,4,4, the mode would be 4. It is possible to have multiple modes depending on the values of the data set.
Normal Distribution
A normal distribution is a describing term which states the majority of the data clusters around the mean. Gaussian Distribution is another term which means the same thing. Normal distributions are theoretical and displayed by a histogram (Fig. 1).
 |
| (Fig. 1) Image of a normal distribution histogram. Image source: http://www.oxfordmathcenter.com/drupal7/node/300. |
Skewness
Skewness describes the balance of the histogram compared to a normal distribution. There are 3 types of skewness: positive, no skew, negative (Fig. 2). Positive skew is when the outliers in a data set are on the positive side of the mean. Negative skew is when the outliers are on the negative side of the mean. No skew means there is an even distribution of the data. When analyzing skew anything below 1 and above -1 is "acceptable".
 |
| (Fig. 2) Image displaying the 3 types of skewness. Image source: http://www.managedfuturesinvesting.com/managed-futures/news/aisource-news/2015/10/13/what-is-skewness. |
Kurtosis
Kurtosis describes the shape of the histogram in relation to the steepness of the distribution compared to the theoretical "normal distribution. Leptokurtic, Mesokurtic, and Platykurtic are 3 different terms which describe Kurtosis. Leptokurtic is a description of a very peaked distribution. Mesokurtic is the description of a "normal distribution. Platykurtic describes a flat distribution. Additionally, Platykurtic is described as negative Kurtosis and Leptokurtic is positive Kurtosis. An example of all three types of Kurtosis can be seen in Fig. 3. When analyzing Kurtosis calculations anything greater than 1 is Leptokurtic and below -1 is Platykurtic.
 |
| (Fig. 3) Image displaying the various forms of Kurtosis. Image source: http://mathsstatistics.weebly.com/unit-2.html. |
Standard Deviation
Standard Deviation is a statistical measurement which describes how spread out the numbers in a data set are from the mean. "1 Standard Deviation" from the mean is equal to 68.2% of the values in a data set. "2 Standard Deviations" from the mean is equal to 95.4% of the values in a data set. "3 Standard Deviations" from the mean is equal to 99.7% of the values in a data set. See Fig. 4 for a visual representation of standard deviation. Standard deviations can go well past 3 depending on the data set.
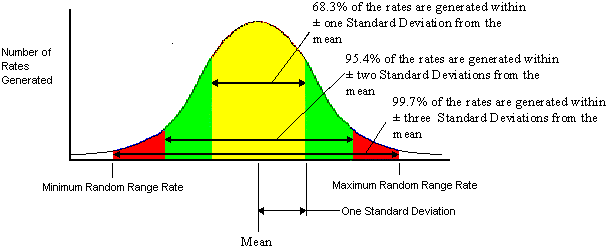 |
| (Fig. 4) Graphical representation of standard deviations. Image source: http://www.jlplanner.com/html/stddev.html. |
There are 2 different ways to calculate standard deviation. If you have a complete data set (one which is not missing any data) you utilize the population standard deviation formula (Fig. 5). If you have a incomplete data set (missing some values or you were not able to sample everyone/everything) you utilize the sample population standard deviation formula (Fig. 6).
 |
| (Fig. 5) Population standard deviation formula. Image source: https://thekubicle.com/lessons/variance-and-standard-deviation. |
 |
| (Fig. 6) Sample population standard deviation formula. Image source: https://spreadsheetsolving.com/sample-standard-deviation/. |
Assignment Description (Part 1)
For the assignment I was given the following scenario:
The question I am to answer is the following:Cycling is often seen as an individual sport, but it is actually more of a team sport. You are looking to invest a large sum of money into a cycle team. While having a superstar is nice and brings attention, having a better team overall will mean more money in your pocket. In the last race in the TOUR de GEOGRAPHIA, the overall individual winner won $300,000, with only 25% going to the team owner, but the team that won, gained $400,000 in a variety of ways, with 35% going to the team owner.Using the incredible set of knowledge learned in your Quant Methods class at UWEC, you decide to put it to good use. You have data (total time for entire race) for teams and individual racers over the last race held in Spain. To begin your investigation you are to analyze the race times of members from the team. Traditionally Team ASTANA has typically produced the race winner (meaning the rider that finishes first), but an up and coming group named Team TOBLER has been making waves on the cycling circuit.
Should you invest in Team ASTANA or gamble on Team TOBLER? Why did you pick one team over another? What descriptive statistics do you think best help explain your answer? Please explain your results using the statistics to support your answer **Please explain results in hours and mins.
 |
| (Fig. 7) Data of race times provided to me by my professor. |
Methods
For this assignment I had to calculate the Range, Mean, Median, Mode, Kurtosis, Skewness, and Standard Deviation for the race times provided to me. I was instructed to calculate the Standard Deviation by hand and all of the other values could be calculated in Excel.
I copied the provided data and imported it into Excel so I could sort the numbers in descending order. I then copied each teams times on my paper. I then calculated the Range, Mean, Median, Mode, Kurtosis, Skewness for each team using Excel.
The next step was to calculate the standard deviation for each team (Fig. 8-9). Since I was provided all of the times for each team I then utilized the "Population Standard Deviation" formula.
 |
| (Fig. 8) Hand calculations of Team Tobler standard deviation. |
 |
| (Fig. 9) Hand calculations of team Astana standard deviation. |
The final step was to analyze the results from the calculations to answer the questions. Additionally, I utilized Excel to verify my hand calculations were correct.
Results
 |
| (Table 1.) Results of calculations for the race teams. |
Discussion and Answer
I don't feel as I have enough data to answer the question I was given. One race result is not enough for me to make a determination of which team I would invest money in. Additionally, I don't know how the scoring is calculated for the finishers which plays into which team would be the overall winner. The final question I would have is how my investment is paid back. With a higher percentage going to the "owner" does my return come from the owner or the team amount? However, I still have to pick a team for the purpose of the assignment and provide an explanation.
I would choose Team Astana based off the data I was provided. The total time (sum) was equal to 569 hours and ~10 minuets compared to Tobler which had a total time of 571 hours and ~21 minuets. While Team Astana had a shorter overall time, I am not sure how points are awarded for the team results. If consistency and closeness in relationship to other members of the team plays into the calculation I would change my answer to Tobler. The Kurtosis result for team Tobler was higher meaning the team members finished very close together. Additionally, the low standard deviation displays the closeness which team Tobler finished with each other. Even though team Tobler had a lower standard deviation meaning the team finished the race closer to each other, the majority of team Tobler finished behind team Astana. The high standard deviation of Astana was related to racer K who finished 20 minuets behind anyone from either team. More data would be need to see if this was a normal occurrence or if racer K just had a bad day or had possibly crashed during the race. Finally, the negative Skewness for Tobler tell me more people finished behind there were a few people behind the average which helps display why the majority of Tobler finished behind Astana.
Part 2
Part 2 of the assignment will have me calculating the mean center and a weighted mean center for the population of Wisconsin by county for 2000 and 2015. First I will provide definitions for both terms before displaying and discussing the results which will be displayed on a map.
Mean Center
Mean center is the average "location" of points which have an X and a Y value and are plotted on a graph or Cartesian Plane (Fig. 10).
 |
| (Fig. 10) Image displaying a calculated mean center for X,Y coordinates. Image source: http://resources.esri.com/help/9.3/arcgisdesktop/com/gp_toolref/spatial_statistics_tools/mean_center_spatial_statistics_.htm |
Weighted Mean Center
Weighted mean center is based off the average like "mean center". However, weighted mean center the points have weights assigned to them by "frequencies" or numbers attached to them. Example if the points had populations data attached to them, the higher the population the higher the weight would be attached to a given point (Fig. 11).
 |
| (Fig. 11) Image displaying the difference in mean center and weighted mean center. Image source: http://support.esri.com/other-resources/gis-dictionary/term/weighted%20mean%20center |
Results
Discussion
You can see the "mean center" is centrally located in the state when analyzing the map in the results section. The mean center is calculated off of the center point of each county, which is why it is located in the center of the state. However, you can see the weighted mean centers are south and a little to the east of the mean center. The weighted mean center takes into consideration the population of the counties. The reasoning for the shift in placement would be the higher populations in southern portion of the state specifically Milwaukee area which is on the south east border of the state. The 2015 weighted mean center moved slightly to the north and the west. The increase of people working in Twin Cities and living the western portion of Wisconsin is one possible cause of this shift.
